What is the radius of curvature of a lens
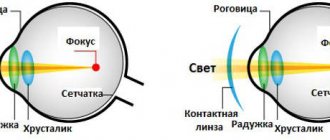
The radius of curvature of a contact lens is a key characteristic that determines the curvature of the inner surface of a contact lens, which is usually designated BS or BC on the packaging.
The radius of curvature of the lens is different for each person and depends on the parameters of the eyeball and is determined strictly individually.
The standard characteristics of the human eye correspond to a lens radius equal to 8.6 . In optical stores, contact lenses with indicators in the range from 8.3 to 8.8 are always available.
In case of significant deviations of eye parameters from the norm, you should place an individual order or contact manufacturers specializing in non-standard vision correction products.
At an appointment with an ophthalmologist, you can get advice on this issue and, based on the results of an ophthalmological examination, prepare a sketch of the required lens.
The required radius of curvature of the lens is determined by the doctor during a study using autorefractometry within a few minutes.
It must be remembered that the autorefractometry method based on infrared radiation, used in an ophthalmological examination when selecting lenses, is a very revealing procedure, since in the process of examining the retina of the eye, it allows one to determine the degree of refraction between the eyes and the degree of astigmatism.
Curvature. Formula for calculating curvature. Circle, center and radius of curvature.
Curvature
When moving along a curve, its tangent changes direction. The speed of this rotation (the ratio of the angle of rotation of the tangent over an infinitely small period of time to this interval) with uniform, unit speed, movement along the curve is called the curvature of the curve. The time derivative of the positive unit tangent vector is called in this case the curvature vector of the curve. Both are functions of a point on a curve. Curvature is the absolute value of the curvature vector.
In the case of an arbitrary parametric definition of a curve[2], the curvature of the curve in three-dimensional space is determined by the formula
,
where is a vector function with coordinates .
In coordinates:
For a curve in a higher-dimensional space, one can replace the cross product, indicated here by square brackets, with the outer product.
Also, for a curve in any dimension of space, you can use the formula for the curvature vector:
and the fact that the curvature is its modulus, as well as the expression for the unit tangent vector
And
and get the formula for curvature:
or, opening the parentheses:
Straight lines and only straight lines have curvature equal to zero everywhere. Therefore, curvature clearly shows how much (at a given point) the curve differs from a straight line: the closer the curvature is to zero, the smaller this difference is. The curvature of a circle of radius R is 1/R.
A doubly differentiable curve has a single osculating plane at every point where the curvature is non-zero.
For plane curves, one can distinguish the direction of rotation of the tangent as one moves along the curve, so curvature can be assigned a sign depending on the direction of this rotation. The curvature of a plane curve given by the equations is determined by the formula
.
The + or - sign is taken by convention, but is preserved along the entire curve.
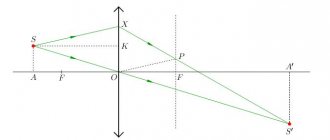
Definition 8.3 The radius of curvature of a curve at a point is the number , where is the curvature of the line at the point . If the curvature at a point is equal to 0, then the radius of curvature is formally set to be equal to .
Note that for a circle, this definition gives the value of the radius of curvature, which coincides with the radius of the circle (constant at all points of the circle).
Without proof, we will report that of all the circles touching a line at a fixed point, the circle that most closely fits24 to the line is the one that has a radius equal to the radius of curvature of the curve at point and convexity in the same direction as the curve. This circle is called the circle of curvature of the line at the point.
Fig. 8.6. Circles tangent to the line and the circle of curvature
Example 8.7 The radius of curvature of a parabola at its vertex is . This means that a circle of radius with a center at a point best approximates a parabola in the vicinity of its vertex, that is, for a parabola it is a circle of curvature at the vertex of the parabola.
Arithmetic properties of derivative
Derivative of the inverse function.
Let the function y=f(x)
is differentiable and strictly monotone on
(a,b)
.
Let also at the point x0?(a,b)
the derivative
f '(x0)≠0
.
Then at the point y0 ?f(x0)
a differentiable function
g(y) is defined,
which is called the inverse to
f(x)
, and its derivative is calculated by the formula
Taylor's formula.
Let the function f ( x) have derivatives of order n + 1 at the point a and some of its neighborhoods. Let x ≠ a be any value of the argument from the indicated neighborhood, then between the points a and x there is a point c such that the formula is valid
5.Function f(x)
is called continuous
at a point a
if it is defined at this point and (1)
The continuity condition (1) can also be written as (2) Function f(x)
is continuous on a set if it is continuous at every point of this set.
If the continuity of a function is broken at some point, then such a point is called a break point .
Discontinuity points can be classified according to the magnitude of the difference between one-sided limits, which is called the jump of the function when passing through point a. If this jump is zero, but the function f(x)
is not defined at point
a
, then such a point is called a removable discontinuity point.
For example, the function f(x)=sin x/x
is not defined at zero, but its limit at this point exists and is equal to 1. Therefore, to eliminate the gap, it is enough to further define the function
f(x)
at x = 0, based on continuity considerations: B In the case of an arbitrary function
f(x)
, for which point
a
is a point of removable discontinuity, it is necessary to expand the domain of definition of the function by including point
a
and assuming If the jump of the function at point
a
has a finite value, then this point is called a discontinuity point of the first kind.
The jump of a function at point a
is equal to infinity if any one-sided limit is equal to infinity.
In this case, we speak of a discontinuity point of the second kind.
Why is it important to choose lenses individually?
Sometimes wearing lenses is accompanied by a feeling of discomfort and even deterioration of vision.
These negative processes are caused by incorrect selection of contact lenses, the radius of curvature of which does not correspond to the individual structure of the eyeball.
Contact vision correction should always be carried out individually , since the degree of comfort and preservation of the patient’s vision depends on the correct fit of the contact lens on the eye.
If the radius of curvature of contact lenses differs from the radius of the cornea, this will cause discomfort to the user and weakened vision..
Ophthalmometry technique
The procedure is completely painless and takes minimal time. No special patient preparation is required. The only condition is the need to remove glasses and contact lenses.
Progress of the procedure:
- The patient is seated on a chair in front of the diagnostic device, the chin is fixed on a special stand.
- The gaze is directed to the required point on the device. Based on the image reflected by the cornea, the computer apparatus calculates the radius of curvature.
- The interpretation of the results is carried out by the doctor who conducted the study.
Opera stores all passwords in the file wand.dat
, which is located in the directory:
- C:\Documents and Settings\Username\Application Data\Opera\Opera (if Windows XP);
- C:\Users\Username\AppData\Roaming\Opera\Opera (if Windows 7,Vista).
This directory stores bookmarks, history, and various browser settings. Copy and save these files as necessary if, after reinstalling, you need to get a new Opera with the old settings.
In order to decode the password from the wand.dat file, you can use a special program, for example OperaPassView
. A very simple program that does not require installation. Just run it and it will give you a list of all passwords and logins. For convenience and reliability, you can save all this into a text document. This way, you will also have a list of all your logins and passwords.
Files where other documents are stored in Opera:
1. Wand.dat -> All passwords.
2. Cookies4.dat -> These are all cookies (links to files that have been cached). 3. Global.dat -> This is the file where all the history is stored. 4. Vlink4.dat -> This is a file that stores the history of visited addresses. 5. Download.dat -> This is a file that stores records of files downloaded through Opera. 6. Notes.adr -> All Notes. 7. Opera6.adr -> All Bookmarks. 8. Widgets.adr -> This file is responsible for writing the paths to Widgets, and for their performance - it is not in the eight. 9. Opcert6.dat -> Personal certificates. 10. Opssl6.dat -> SSL settings. 11. Opera.dir -> This file stores all the typed addresses in the address bar. 12. Search.ini -> File responsible for search engines in Opera. 13. Files with the extension *.lng -> are responsible for translation in Opera (they are located in the root folder of Opera). Directories:
1. Directory “Images” -> Directory where icons of launched pages (sites) are stored, as well as icons of bookmarks and sidebars. 2. Directory “Sessions” -> Directory where saved sessions (sessions) are stored. 3. Directory “Skin” -> Directory where skins (skins) for Opera are stored. 4. Directory “Widgets” -> Directory where Widgets files are stored - it is not in the eight. 5. Directory “Cache4” -> Directory in which the entire cache is stored (cached files and Opera pages). 6. Directory “Mail” -> Directory where mail files and news feeds - RSS are stored (this directory is in the Opera root folder).
Sources:
compcapital.ru - Where Opera stores passwords, bookmarks, etc.;
posovet.ru - Where does Opera store passwords?
Proper contact lens fit
In addition to the radius of curvature, it is important to pay attention to what material the lens is made of, since different materials have different mobility on the cornea. The norm for this indicator is from 0.5 mm to 1.5 mm.
It is better to choose silicone hydrogel lenses because they have high oxygen permeability compared to hydrogel lenses. It is very important that tear exchange under the lens occurs normally, and that the lens is regularly cleaned of dead epithelial cells, lactic acid and other accumulations.
Manifestation of incorrectly selected lens curvature
If the curvature of the lens deviates by 0.2 units, a person may not feel any discomfort, so such lenses are allowed to be worn. But when the indicator is significantly higher, wearing lenses is prohibited.
A smaller radius of curvature leads to difficult lens mobility. This causes the eyes to constantly strain, the blood vessels are compressed and, as a result, the eyes turn red. Sometimes, due to the lens lying too tightly on the eye, tears cannot penetrate through it, an inflammatory process begins, the cornea swells, and vision gradually deteriorates.
A larger radius makes the lens very mobile, which leads to its loss, excessive tearing and damage to the cornea itself. The person will feel pain when blinking, as well as instability of vision. This lens fit is called flat.
There are situations when the lenses initially fit a person, but after a while they take on a flat or, conversely, convex fit. Therefore, after purchasing lenses, you need to visit your doctor again two weeks later. You can also check with an ophthalmologist every time you buy new lenses.